|
For φ= 1, dvs. 100% mættet luft benævnes den dertil svarende temperatur for dugpunkt eller dugpunktstemperatur. Tilførsel af mere vand eller en køling til en lavere temperatur, vil resultere i udkondensering af vand. Modsat fordamper vand kun i en atmosfære, hvor φ er mindre end 1. Ligesom man ved kompression - som nævnt i foregående eksempel - kan hæve den relative fugtighed og dermed dugpunktet, kan man ved ekspansion sænke dugpunktet.
Eksempel: Ved P1 = 7 Bar abs. er dugpunktstemperaturen f.eks. t1 = 2°C. Hertil svarende ps1 = 7,05 mBar jvf, tabel 7.1.
φ2 = φ1l x Ps1/Ps2 x P2/P1
Ps2 = φ1/φ2 x ps1 x P2/P1
Da vi taler om dugpunkt, har vi 100% mætning og φ1 = φ2
Ved ekspansion til P2 = 1 Bar bliver ps2 = ps1 x P2/P1 = 7,05 x 1/7 = 1,007 mBar
til ps2 svarer iflg. tabel 7.1 dugpunktstemperatur tau2 = -23°C.
FUGTIGHEDSGRAD/BLANDINGSFORHOLD
Fugtighedsgrad/blandingsforhold angiver i hvilket forhold vandmængde og tør luft er blandet:
x = gram vand / kg tør luft
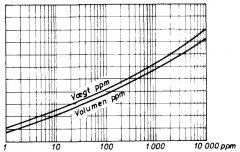
PPM
PPM er en fugtighedsbetegnelse indført fra Amerika. Den er ikke umiddelbar hensigtsmæssig, men anvendes og må derfor nævnes. PPM (parts pr. million) angives såvel i forhold til volumen som i forhold til vægt, og i begge tilfælde i forhold til tør luft.
 MÆTNINGSGRAD
Mætningsgrad er forholdet mellem fugtighedsgrad i umættet og mættet tilstand:
MG=x/xm
MG er ved atmosfæretryk og temperaturer under ca. +50°C tilnærmelsesvis lig med φ
MAXIMAL MÆTNING
Ved atmosfæretryk og 100°C er 100% mætning netop mulig, idet kun vanddamp og ingen luft mere er til stede. Dette iflg. Dalton fordi pw = ps = 1,013 Bar abs. Over 100°C er φ mindre end 100 %.
NORMALTILSTAND - NORMALKUBIKMETER
For at kunne angive en lufttilstand entydigt, har vi vedtaget at bruge en tilstand, hvorfra andre tilstande kan beregnes.
Vor normaltilstand er baseret på:
Temperatur 20°C
Tryk 1,013Bar(=1013HPa)
RF 60%
og 1 m3 luft ved denne tilstand betegnes da
1 Nm3 = 1 Normalkubikmeter
VANDINDHOLD I ANDRE GASSER END LUFT
Blandingen af en gas og vanddamp betragtes som en blanding af 2 gasser, og Daltons lov er gældende. Det betyder, at den ene gas’s tilstand er uafhængig af mængde og tryk af den anden. Når blandingens tryk, temperatur og fugtighedsgrad er kendt, kan vandindholdet beregnes.
Eksempel: For tilstanden +30°C, 80% RF ved 1013 mBar er:
Fugtighedsgraden x = 21,8 glkg og vægtfylde af luften Rho = 1,13 kg/m3
Heraf kan den absolutte fugtighed beregnes:
f = 21,8 x 1,13 = 24,63 g/m3
Denne værdi er uafhængig af trykket og er den samme for enhver gas, ved ethvert tryk ved +30°C og 80% RF ønskes vandindhold beregnet i g/kg skal gassens vægt beregnes under de givne forhold og således:
Molvægten af enhver gas ved 0°C og 1,013 bar har et rumfang på 22,4 m3.
For CO2 f.eks. er Molvægten = 44.
CO2’s vægtfylde ved 0°C og 1013 mbar er da:
44/22,4 = 1,964 kg/m3
Ved +30°C og 5 Bar overtryk er vægtfylden:
6/1,013 x 273/(273+30) x 1,964 = 10,481 kg/m3
Og fugtighedsgraden:
x = 24,63/10,481 = 2,35 g/kg
I beregninger af fugtighedsgraden må det huskes, at vanddampenes mætningstryk er uafhængig af totaltrykket, hvorfor den relative fugtighed φ og den abs.fugtighed stiger proportionalt med trykket ved samme temperatur.
φ2 = φ1 x P2/P1
Såfremt φ2 overstiger 1 sker kondensation. Omvendt bevirker en ekspansion, at den absolutte og den relative fugtighed reduceres proportionalt. Dog under forudsætning af, at ekspansionen ikke sker så pludseligt, at der opstår en temperatursænkning. |
|